Etiket arşivi: vector calculus

Silindirik koordinatlarda diverjans

Bir Cevap Yazın

Kartezyen koordinatlarda vektör alanının diverjans aşağıdaki gibi tanımlanıyor.

\mathbf F = (F_x, F_y, F_z) \newline\newline \nabla\cdot \mathbf F = \left(\frac {\partial} {\partial x},\frac {\partial} {\partial y},\frac {\partial} {\partial z}\right) \cdot\left(F_x, F_y, F_z\right)= \frac {\partial F_x} {\partial x}+\frac {\partial F_y} {\partial y}+\frac {\partial F_z} {\partial z}

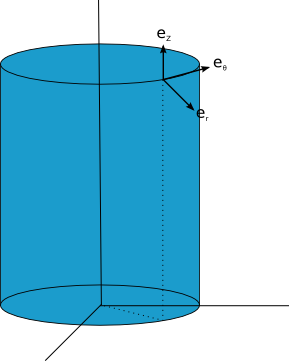
Kartezyen koordinatlar cinsinden silindirik koordinat birim vektörleri tanımlanabilir

Silindirik birim vektörler

Silindirik koordinatlar r, \theta,z cinsinden tanımları:

x = r.cos(\theta)\newline y = r.sin(\theta)\newline z = z

e_z, \mathbf k ile aynı: e_z = (0, 0, 1)

e_r = \frac {\left(x, y, 0\right)} {\sqrt{x^2+y^2}} = \frac {\left(r.cos\left(\theta\right), r.cos\left(\theta\right), 0\right)} {r} = (cos(\theta), sin(\theta), 0)

e_\theta ise bu iki vektörün vektörel çarpımına eşittir.

e_\theta = e_z \times e_r = \frac {(-y, x, 0)} {\sqrt{x^2+y^2}} =(-sin(\theta), cos(\theta), 0)

Şimdi vektör alanını x, y ve z yerine r, \theta,z şeklinde yazabiliriz.

\mathbf F = (F_r, F_\theta, F_z) = F_re_r + F_\theta e_\theta + F_ze_z \newline\newline \mathbf F = F_r(cos\theta, sin\theta, 0) + F_\theta(-sin\theta, cos\theta, 0) + F_z(0, 0, 1) \newline\newline \mathbf F = (F_rcos\theta - F_\theta sin \theta, F_rsin\theta + F_\theta cos \theta, F_z)

Şimdi del operatörünü r, \theta,z cinsinden yazmak için zincir kuralını kullanacağız.

\frac {\partial} {\partial r} = \frac {\partial} {\partial x} \frac {\partial x} {\partial r} + \frac {\partial} {\partial y} \frac {\partial y} {\partial r} \newline\newline \frac {\partial} {\partial \theta} = \frac {\partial} {\partial x} \frac {\partial x} {\partial \theta} + \frac {\partial} {\partial y} \frac {\partial y} {\partial \theta}

Aşağıdaki türevleri biliyoruz.

\frac {\partial x} {\partial r} = cos\theta\newline\newline \frac {\partial y} {\partial r} = sin\theta\newline\newline \frac {\partial x} {\partial \theta} = -r.sin\theta\newline\newline \frac {\partial y} {\partial \theta} = r.cos\theta\newline\newline

Bunları yerlerine koyup gerekli düzenlemeleri yaparsak del operatörü aşağıdaki gibi olur.

\nabla = \left( \frac 1 r \left( r.cos\theta\frac {\partial} {\partial r} -sin\theta\frac {\partial x} {\partial \theta}\right), \frac 1 r \left( r.sin\theta\frac {\partial} {\partial r} +cos\theta\frac {\partial x} {\partial \theta}\right), \frac {\partial} {\partial z}\right)

O zaman diverjans formülü şu şekilde yazılabilir.

\nabla\cdot F = \left( \frac 1 r \left( r.cos\theta\frac {\partial} {\partial r} -sin\theta\frac {\partial x} {\partial \theta}\right), \frac 1 r \left( r.sin\theta\frac {\partial} {\partial r} +cos\theta\frac {\partial x} {\partial \theta}\right), \frac {\partial} {\partial z}\right)\cdot (F_rcos\theta - F_\theta sin \theta, F_rsin\theta + F_\theta cos \theta, 0)

Açılınca ise

\nabla\cdot F = \frac 1 r \frac {\partial} {\partial r} F_r r.cos^2\theta \newline\newline - \frac 1 r \frac {\partial} {\partial r}F_\theta cos\theta sin\theta \newline\newline - \frac 1 r \frac {\partial} {\partial \theta} F_r cos\theta sin\theta \newline\newline + \frac 1 r \frac {\partial} {\partial \theta} F_\theta sin^2\theta \newline\newline + \frac 1 r \frac {\partial} {\partial r} F_r r.sin^2\theta \newline\newline + \frac 1 r \frac {\partial} {\partial \theta} F_\theta cos\theta sin \theta \newline\newline + \frac 1 r \frac {\partial} {\partial \theta} F_r cos\theta sin\theta \newline\newline + \frac 1 r \frac {\partial} {\partial \theta} F_\theta cos^2\theta \newline\newline + \frac {\partial} {\partial z} F_z

Böylece sonuç aşağıdaki gibi çıkıyor:

\nabla\cdot F = \frac 1 r \frac {\partial (r.F_r)} {\partial r} + \frac 1 r \frac {\partial F_\theta} {\partial \theta} + \frac {\partial F_z} {\partial z}